NP vs P Project
My full paper on the P vs NP space discussing the problem set as well as my implementation and approach to efficiently solving the Traveling Salesman Problem (TSP) can be found here or below.
Overview
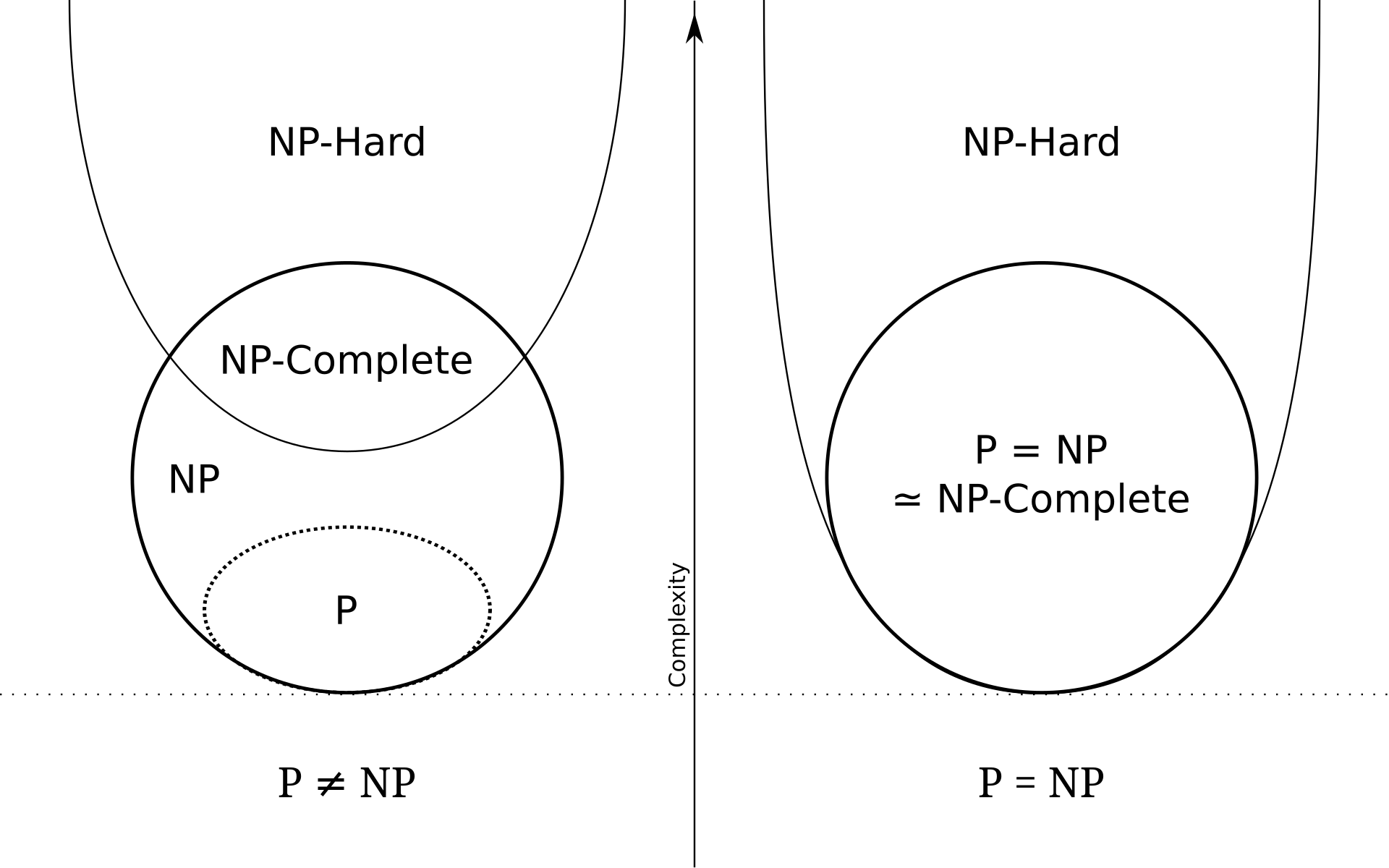
The brief idea of P vs NP revolves around the idea of certain problems being solvable in polynomial time while others are nondeterministic polynomial, meaning an answer can not necessarily be found quickly. The P vs NP problem is considered solved when we are able to either prove that P = NP or that P != NP. If we can show that P = NP we are able to solve many "hard" problems. This is because all the problems within the NP space are reducible to every other proble within the NP space, hence showing a reduction from NP to P would be a huge development in the field.
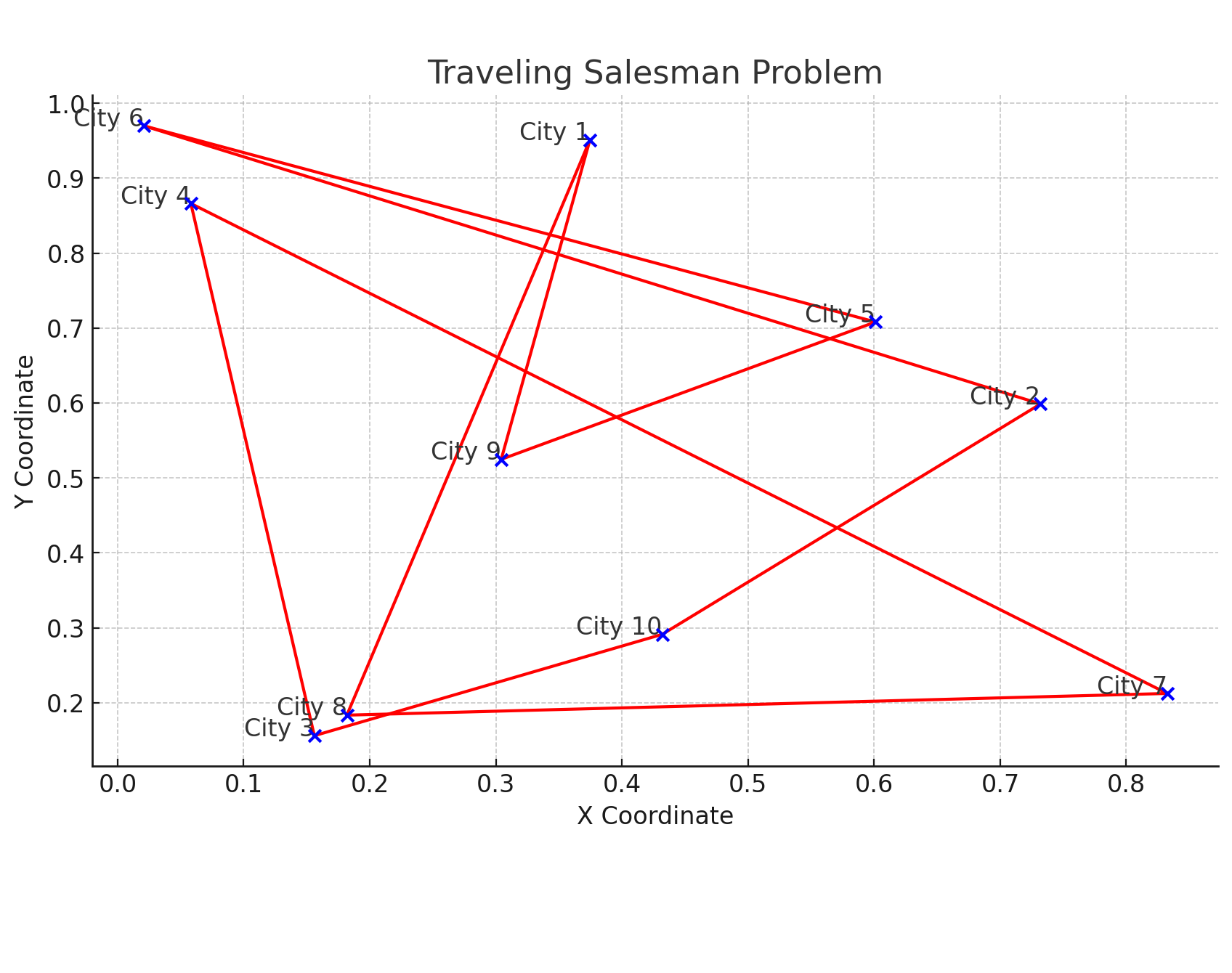
Traveling Salesman Problem (TSP)
For the TSP I was engaged in a competition to develop a heuristic solution to solving the TSP efficiently. The idea of the TSP is a salesman is given a list of cities he must visit, he can travel from any city to any other city visiting each a single time, but each leg of the journey has a cost associated with it. The salesman must find the optimal route to travel between these cities. The problem becomes a graph problem with each edge having a weight. I developed an algorithm in Python using known heuristic methods starting from various nodes multithreaded. My idea was that starting from different positions in the graph would yield vastly different results, and multithreading would allow these calculations to be done in parrallel. I entered my algorithm in a university competition aimed at finding an optimal solution to the problem.
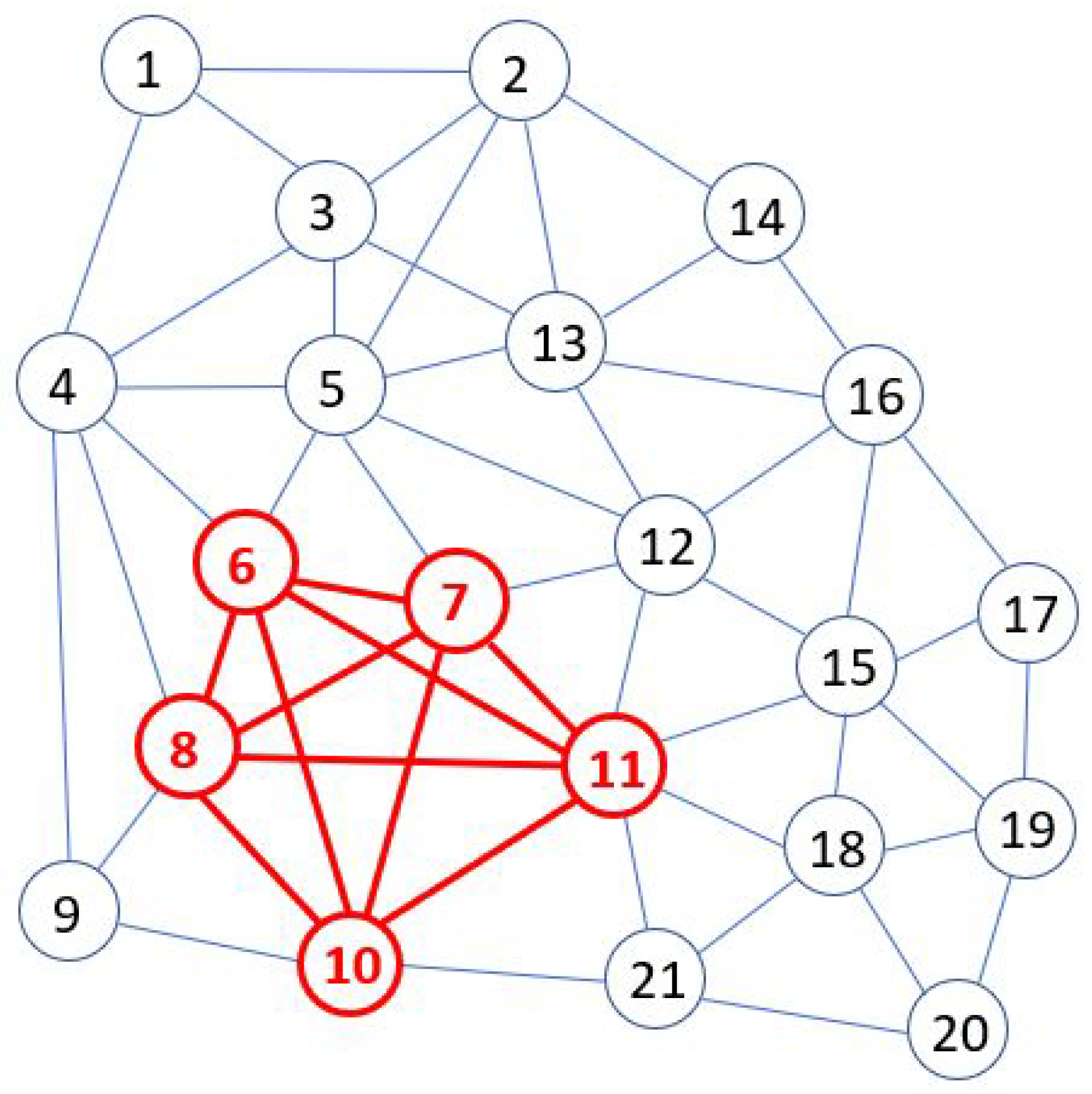
Max-Clique
Similar to the TSP I also developed a and entered a solution into the competition for another NP problem the Max-Clique. The Max-Clique problem is another graph based problem where within a graph you must find the largest number of fully connected nodes. E.g. In the graph to the right the set of 5 red nodes represent the largest clique within the graph. Similar to my solution to TSP I utilized